本文介绍Self-attention的原理以及常见问题。
Self-attention用于提取序列特征
Self-attention机制是一种计算单个序列各个元素之间关联性的方法,例如给定一个输入序列:”Hello,I love you!”,通过self-attention机制可以计算单词之间的关系,例如”Hello”和”I”之间的关系更为接近,与”you”则没有什么关系。最终可以得到一个这样的得分矩阵,通过这个矩阵我们可以猜测,在出现了文本预测的时候,当输入的是”Hello”的时候,后面接着的是”I”的概率最大。
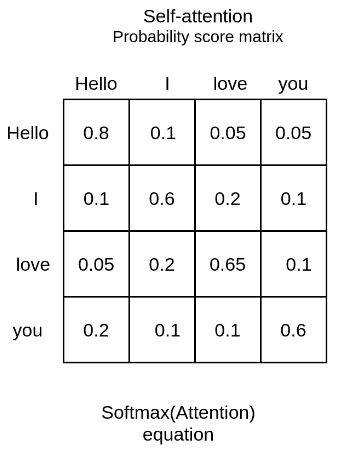
获取attention矩阵
如何得到这样一个矩阵呢?以及得到了这样一个矩阵之后,如何利用这个矩阵对输入数据进行进一步处理呢?我们还以上面这句话为例介绍。
首先在文本处理中,第一步肯定是Embedding,也就是将文本转换为向量。转换的方法很多,包括传统的one-hot encoding,word2vec方法,到现在的BERT,GPT等。比如说我们将”Hello”转换为向量$x^1$,”I”转换为向量$x^2$,”love”转换为向量$x^3$,”you”转换为向量$x^4$。那么如何得到如图1这样的矩阵呢?
这边借用一下李宏毅老师的课件分析一下。对于一排输入向量$\left\lbrack x^1,x^2,x^3,x^4 \right\rbrack$,首先对它们做一下线性变化得到向量$\left\lbrack a^1,a^2,a^3,a^4, \right\rbrack$。得到这样一排向量之后,分别对每一个向量$a^i$乘以$w^q,w^k,w^v$,得到向量$q,k,v$,即大家常说的query,key和value,具体如图2所示。至于如何理解这仨个量,直观理解参考:如何理解Q、K、V?
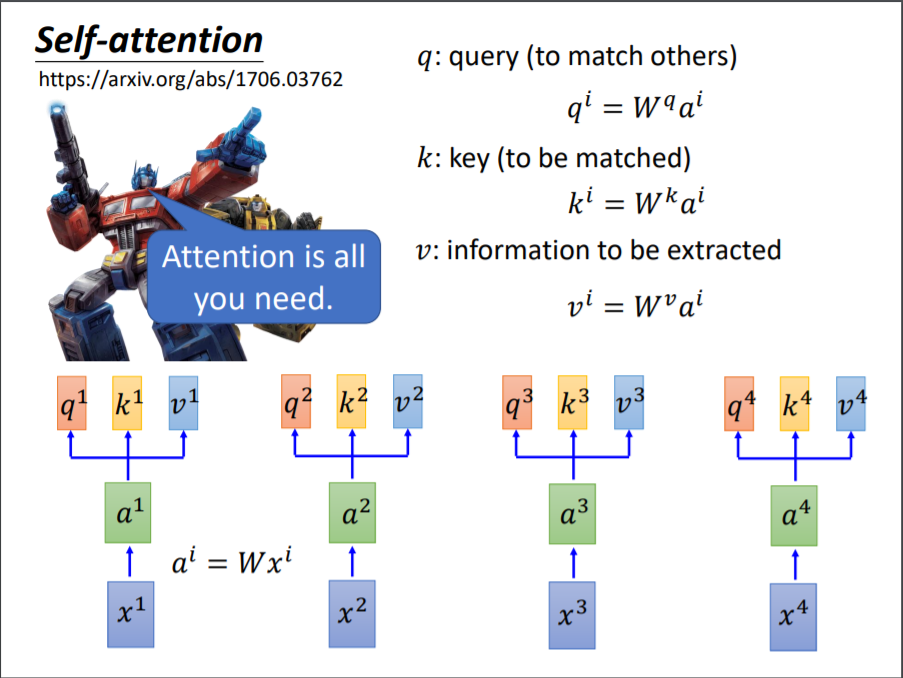
得到了每个向量对应的$q^i,k^i,v^i$后,就可以开始计算attention的数值了,这里采用的是Scaled Dot-Product的方法,具体操作如下:
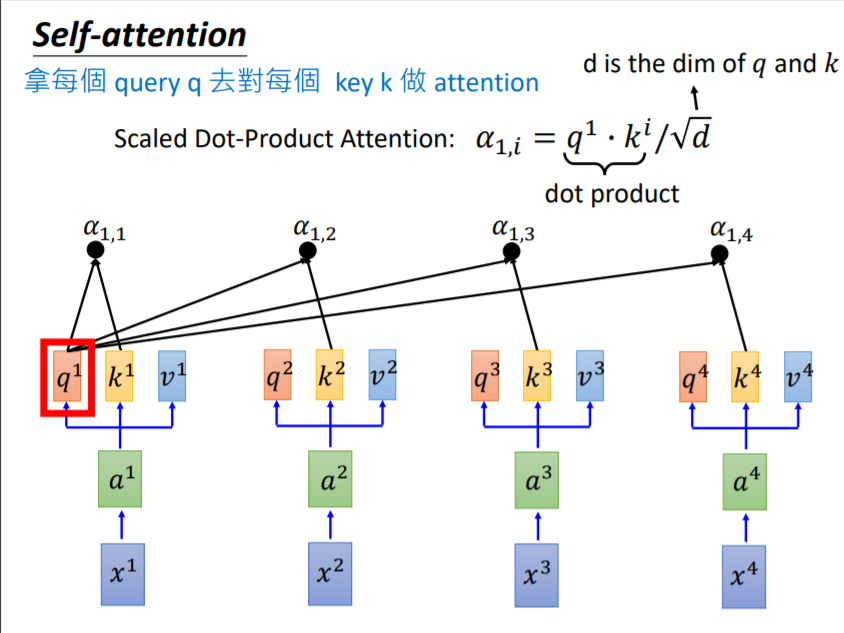
比如说为了计算$x^1$和其他三个向量之间的关联性,用$q^1$乘以包括$k^1$在内的所有$k^i$值,然后再除以$\sqrt{d}$,得到了四个$\alpha_{1,i}$值,这四个值做完softmax之后,就是图1中的第一列(行)的值,过程如图3所示。对所有的向量都做同样的过程,最终就可以得到图1所示的得分矩阵啦。
那么我们就知道了,$q,k$是为了计算得分矩阵的,那么剩下来的$v$,是干什么的呢?其实向量$v$就是保存原始向量$x$信息的,既然有了向量之间的关联性,那么我们用这个作为权重,对向量$v$进行加权,就可以得到每个向量对应的输出啦。如图4所示,输入向量$x^1$最终得到的输出是向量$q^1$。可以想到,$q^1$是和$v^1$最像的,因为在加权平均里$v^1$的权重$\alpha$最大;但是同时,它和$v^1$不同之处在于,它融合了整个序列的其他信息,这样输出的结果表达能力更好。
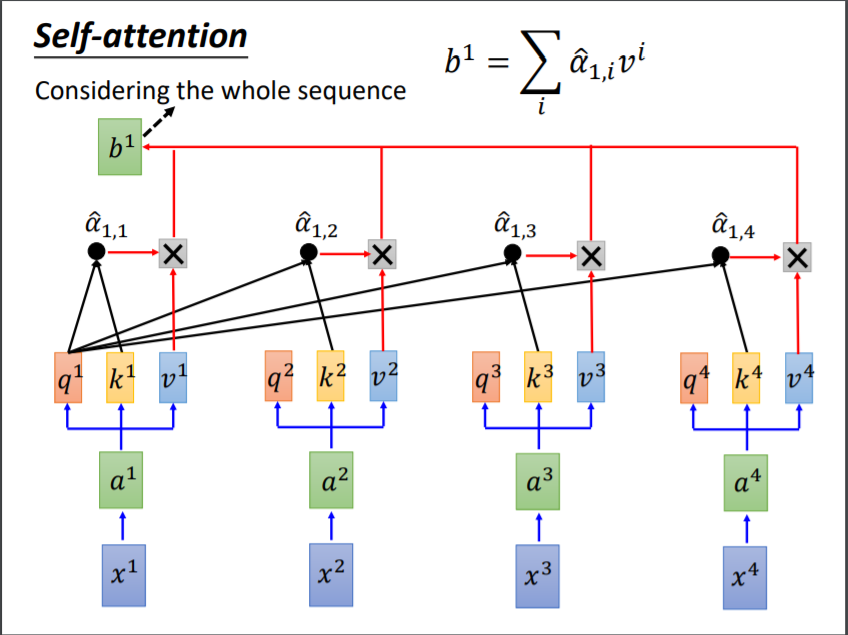
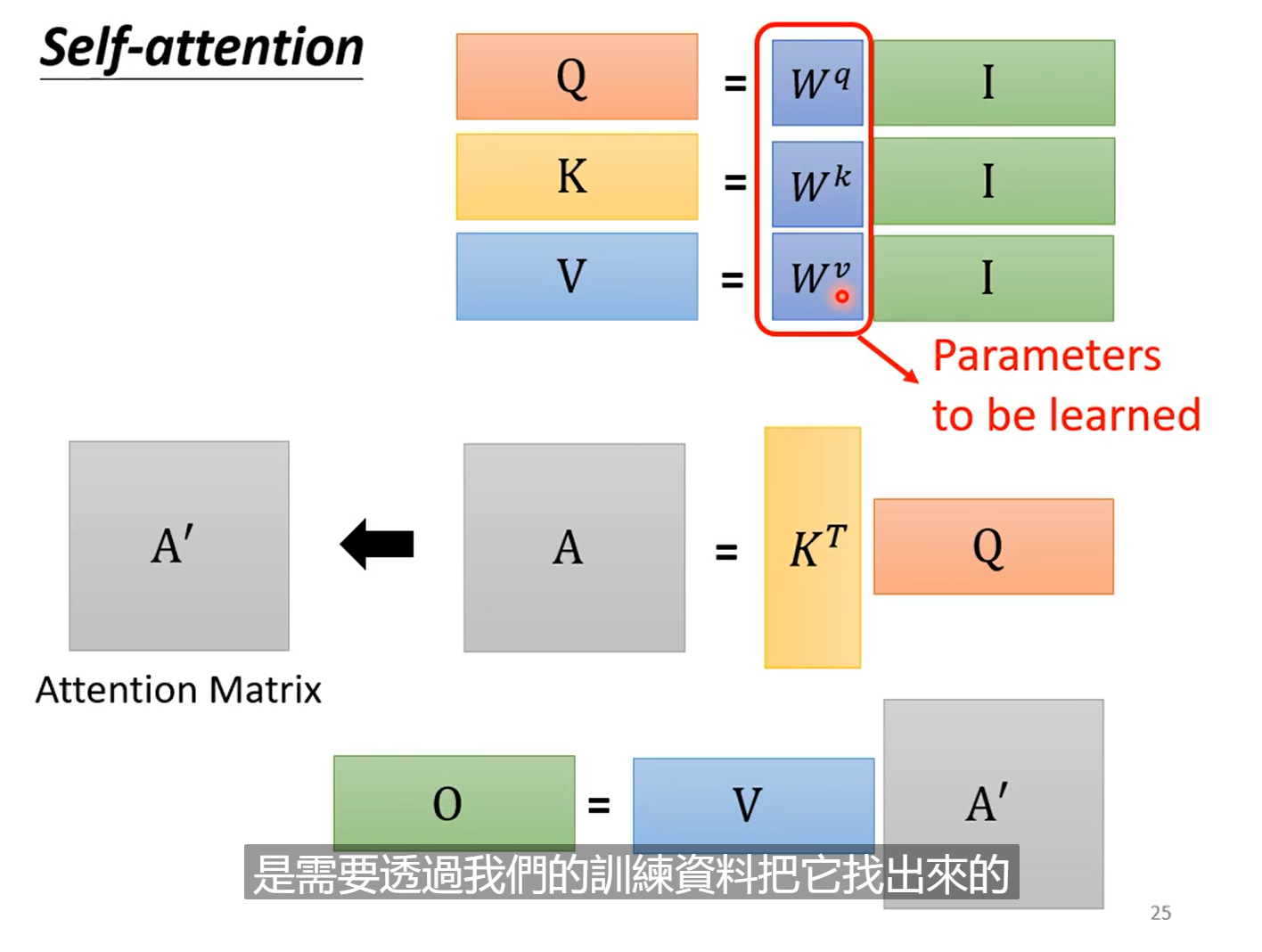
以上是个向量维度的演示,实际做的时候,我们是把向量拼成矩阵,用矩阵的乘法代替向量的乘法,$I$中为输入向量按照列拼成的输入矩阵,$Q$的是$q$按照列拼接起来的,$A$是算出的attention矩阵,$A’$是除以$\sqrt{k}$并做softmax之后的的矩阵,$O$是输出结果。
综合上面的介绍,我们总结一下计算attention的流程,分为如下三个部分:
step1:计算权值系数
采用不同的函数或计算方法,对query和key进行计算,求出相似度或者相关性
采用的计算方法有:
向量点积
cosine相似度
mlp网络
step2:softmax归一化
原因:score值的分布过于分散,将原始计算分值整理成所有的元素权重之和为1的概率分布
利用softmax的内在机制(结果向更大的值偏移)突出重要元素的权重
step3:加权求和
- 每一个向量的输出为所有其他所有value值的加权评价,权值为attention值。
常见问题
为什么用双线性点积模型(即Q,K两个向量)
双线性点积模型使用Q,K两个向量,而不是只用一个Q向量,这样引入非对称性,更具健壮性(Attention对角元素值不一定是最大的,也就是说当前位置对自身的注意力得分不一定最高)
为什么不能$q,k,v$都等于向量$x$,而是要分别乘以不同的向量来得到这么多向量?
使用不同的q,k,v可以保证在不同的空间进行投影,增强了模型的表达能力,提高了泛化性能。
经过self-attention得到的输出在形状上和输入相同,为什么就可以得到更好结果?
输出与输入相比,更多的增加了元素之间的关联特性,这些特性在文本处理中十分有益。
$w_q,w_k,w_v$是如何得到的?
在实际的代码过程中,这一步是通过nn.linear模块得到的,w_q,w_k,w_v则是模块的参数,随着训练的过程而学习到。
为何$q*k$后要除以$\sqrt{k}$,不除行不行?
因为使用softmax进行分类,较大的值梯度较小,且softmax有放大作用会把大部分概率给最大的元素,其他的元素梯度消失;因为原q和k都是满足0均值,1为方差的正态分布的,但是,在向量相乘之后均值仍然为0,方差变为了k,所以除以$\sqrt{k}$。
self-attention如何并行化?
在 self-attention 能够并行的计算句子中不同的 query,因为每个 query 之间并不存在 先后依赖关系,也使得 transformer 能够并行化;
Self-attention与其他模型的比较
我们从三个方面衡量模型的优劣,第一是性能,指标是时间复杂度,第二是可并行性,第二是可并性行行,指标是所需要的最小顺序操作数;第三是处理长依赖的能力,指标是网络中远程依赖项之间的路径距离。
先规定一下参数表示,$n$表示序列的长度,$d$表示每个词的向量维度,$k$表示卷积核的大小,$r$表示限制版自注意力中领域的大小。
| Layer Type | Complexity | Sequential Operations | Max Path Length |
|---|---|---|---|
| Self-Attention | $O(n^2d)$ | $O(1)$ | $O(1)$ |
| Recurrent | $O(nd^2)$ | $O(n)$ | $O(n)$ |
| Convolutional | $O(knd^2)$ | $O(1)$ | $O(log_k(n))$ |
| Self-Attention (restricted) | $O(rnd)$ | $O(1)$ | $O(n/r)$ |
自注意力包括三个步骤:相似度计算、softmax和加权求和。相似度计算的时间复杂度是$O(n^2d)$,因为可以看成(n,d)和(d,n)两个矩阵的相乘。softmax的时间复杂度是$O(n^2)$。加权求和的时间复杂度是$O(n^2d)$,同样可以看成(n,n)和(n,d)的矩阵相乘。
从性能角度说,该模型在序列长度过长时表现不如RNN,不过在可并行性和处理长依赖的能力上具有绝对的优势。我们的任务,就是想办法尽可能用词向量维度来弥补长度的劣势,只要$d<n$,那么模型的性能也是杠杠的。
多头注意力
介绍了以上的基础,下面介绍multi-head self-attention。多头注意力机制看起来只是在单头的基础上,直接把输入中的向量在embedding维度上切分为N份,计算多个N和q,k,v,最后把计算结果取一个均值得到的,这么做的好处包括:
- 并行计算;
- 把句子投影到不同的子空间中,增加模型表达能力。