HelloBear

Less is More

0%

Transformers

Posted on Edited on

本文介绍Transformers代码实现的细节，包括7个部分。

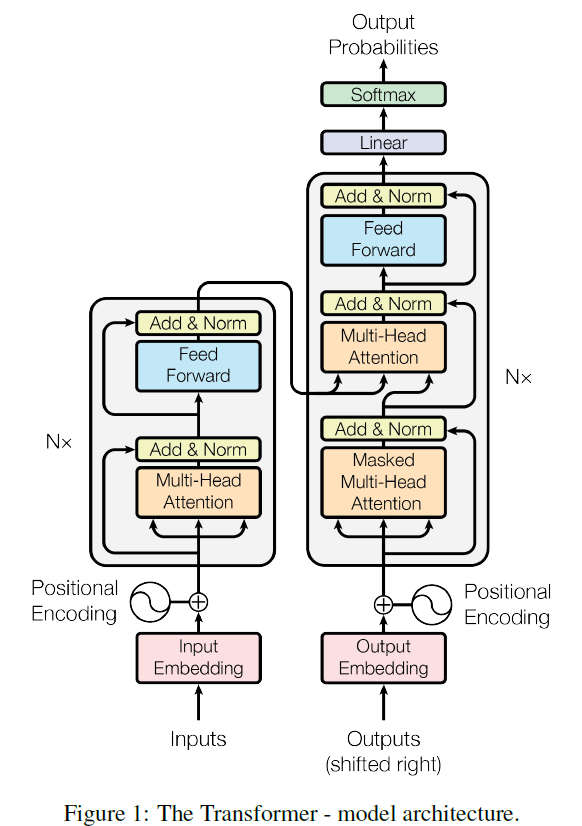
在开始之前，先放上论文中的模型架构，下面的每个部分将依次实现这个架构中的一部分。

Embedding

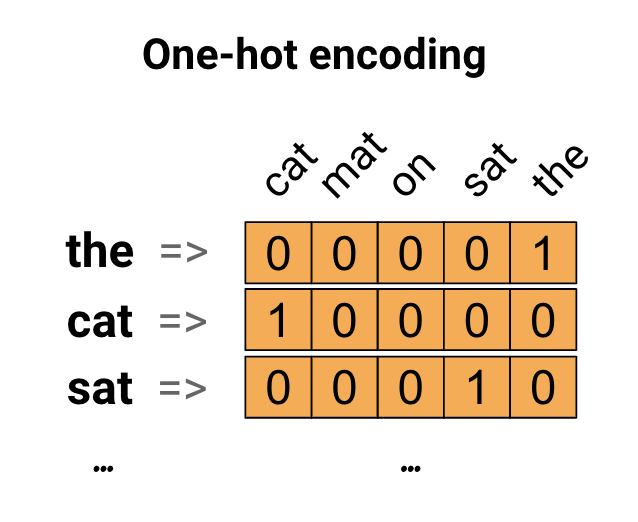
为了处理文本，首先需要对所有的文本进行一个数字化的处理。表示文本的方法都多种，最容易想到的是one-hot编码，如下图所示，这种方法没有考虑到单词之间的关联性，表示能力不强。

在自然语言处理中，现在常用的编码方法是Embedding，它是指，根据单词之间的关系，将每个单词投影到高维度的空间中，词汇用一个数值表示，每个维度代表一种特征。

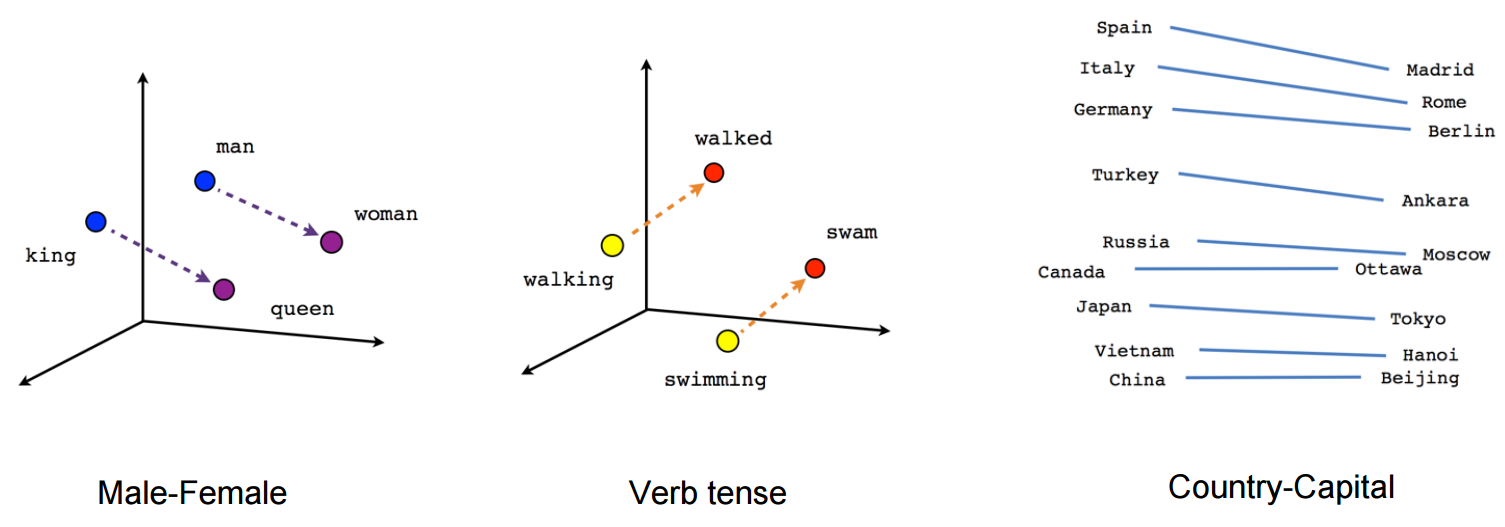
如上图所示，有关联的词汇在embedding之后向量之间的距离更近。Embedding的方法有两种，count based和prediction based，第一种很直观，根据在一篇文章中某些词汇出现的次数来评判词汇之间的关联程度，第二种则是在一句话中，根据前一个或几个词，训练一个神经网络来预测它后面的词汇出现的概率。

总之，Embedding完成之后，相近的单词对应的词向量在空间中的距离就会更近：

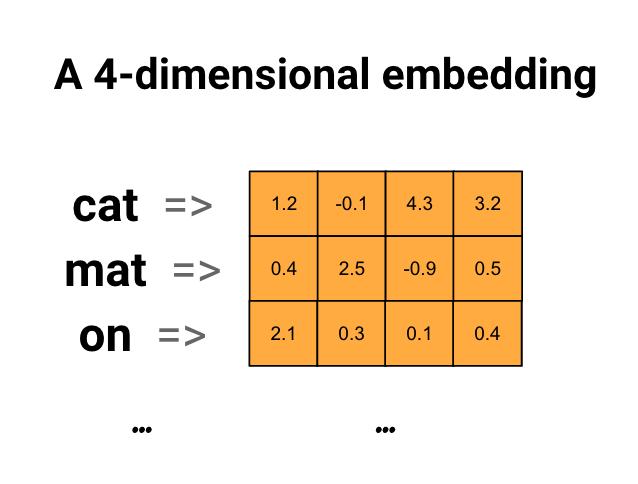
在Pytorch中，Embedding的代码如下：

1
2
3
4
5
6
class Embedder(nn.Module):
    def __init__(self, vocab_size, d_model):
        super().__init__()
        self.embed = nn.Embedding(vocab_size, d_model)
    def forward(self, x):
        return self.embed(x)

The positional encoding

为了使模型能够处理一个距离，它需要了解每个单词的两件事：这个词是什么意思？它在句子中的位置是多少？Embedding得到的向量可以学习词汇的意思，现在需要考虑如何加入单词的位置信息。

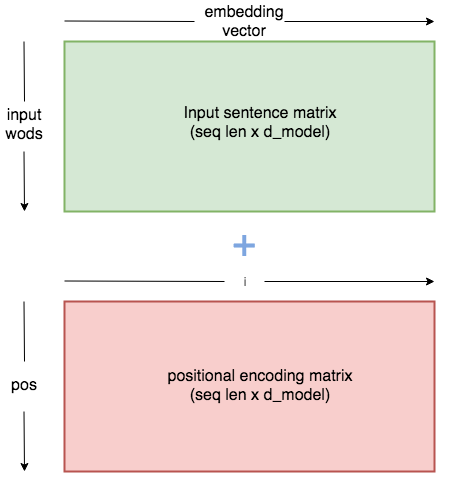
这个问题的答案非常的容易，只需要在embedding得到的二维矩阵基础上加上固定的数值就可以了，如图所示，绿色的方块表示我们得到的二维矩阵，我们用$i$表示在每个词向量的位置，$pos$表示每个单词在一个句子中的位置。

那么positional encoding就很容易了，直接根据如下方式，在输入中加数值，其中$d_{model}$是指Embedding后每个词向量的维数，即图中二维向量的列数。

$$
PE_{(pos, 2i) } =\sin (pos/10000^{ 2i / d_{model} })
$$

$$
PE_{(pos, 2i+1)} =\cos (pos/ 10000^{2 i / d_{model} })
$$

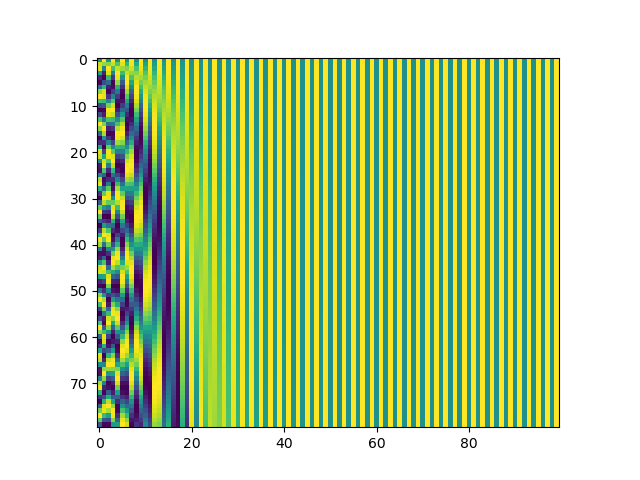
例如给定模型的维数是80，我们画出的position encoding marix如下：

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class PositionalEncoder(nn.Module):
    def __init__(self, d_model, max_seq_len=80):
        super().__init__()
        self.d_model = d_model

        # create constant 'pe' matrix with values dependant on 
        # pos and i
        pe = torch.zeros(max_seq_len, d_model)
        for pos in range(max_seq_len):
            for i in range(0, d_model, 2):
                pe[pos, i] = \
                    math.sin(pos / (10000 ** ((2 * i) / d_model)))
                pe[pos, i + 1] = \
                    math.cos(pos / (10000 ** ((2 * (i + 1)) / d_model)))

        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)

    def forward(self, x):
        # make embeddings relatively larger
        x = x * math.sqrt(self.d_model)
        # add constant to embedding
        seq_len = x.size(1)
        x = x + Variable(self.pe[:, :seq_len], \
                         requires_grad=False)
        return x


# plot the position data
P = PositionalEncoder(100)
print(P.pe)
plt.imshow(P.pe[0])
plt.show()

看到在代码中，我们先增加了原数据的数值之后再加入的位置信息，这样可以使得原数据中的信息可以保留。

对位置编码的解释，主要分为两个方面，一个在pos维度上，为什么要用周期函数（sin和cos），以及在不同的维度上，为什么要用变换不同的周期？

首先，在不同的pos位置上，我们的本意是需要一种表示，它可以体现单词在不同位置的区别，又得体现单词的先后顺序。如果直接采用1-pos的值，那么就会改变原数据的分布，且甚至会比原数据值还大，所以得有一定的值域限制。同时，就算用（1-pos）/ Length也不行，因为这样前面的间隔就大，后面的间隔就小，次序关系被稀释。所以采用了周期函数用于限制值域，且间隔稳定，且同时使用sin和cos可以用积化和差公式解释；在不同的维度上使用不同的频率是为了让高维表示有意义。

Position encoding为什么选择相加而不是拼接呢？

$$
[W_1W_2][e;p]=W_1e+W_2p,W(e+p)=We+Wp
$$

就是说求和相当于拼接的两个权重矩阵共享（W1=W2=W），但是这样权重共享是明显限制了表达能力的，所以这样做主要还是为了较少计算复杂度。

Position encoding和 Position embedding的区别？

  • Position encoding 构造简单直接无需额外的学习参数；能兼容预训练阶段的最大文本长度和训练阶段的最大文本长度不一致；
  • Position embedding 构造也简单直接但是需要额外的学习参数；训练阶段的最大文本长度不能超过预训练阶段的最大文本长度（因为没学过这么长的，不知道如何表示）；但是Position embedding 的潜力在直觉上会比 Position encoding 大，因为毕竟是自己学出来的，只有自己才知道自己想要什么（前提是数据量得足够大）。

为何17年提出Transformer时采用的是 Position Encoder 而不是Position Embedding？而Bert却采用的是 Position Embedding ？

  • Transformer 的作者在论文中对比了 Position Encoder 和 Position Embedding,在模型精度上没有明显区别。出于对序列长度限制和参数量规模的考虑,最终选择了 Encode 的形式。那么为什么Bert不这么干呢？主要原因如下：
    • 模型的结构需要服务于模型的目标：Transformer最开始提出是针对机器翻译任务的，而机器翻译任务对词序特征要求不高，因此在效果差不多的情况下选择Position Encoder 足矣。但是Bert是作为通用的预训练模型，下游任务有很多对词序特征要求很高，因此选择潜力比较大的Position Embedding会更好；
    • 数据量的角度：Transformer用的数据量没有Bert的数据量大，所以使用潜力无限的 Position Embedding 会有大力出奇迹的效果；

Masks

Transformer中的Mask机制主要有两重作用：

  • 在encoder和decoder中，将padding补充的数据对应的attention值设置为0，这很好理解，就是说在计算self-attention时不考虑人为补充的数据；

  • 在decoder中，我们算self-attention时候对于每个单词，我们只考虑它和它之前的单词之间的关联性，而不考虑它之后的单词，因为我们在预测的时候只是拿当前位置之前的句子去预测之后的结果。

具体的代码如下，对于输入序列，只要将padding的位置标记为0就可以了：

1
2
3
4
batch = next(iter(train_iter))
input_seq = batch.English.transpose(0,1)
input_pad = EN_TEXT.vocab.stoi['<pad>']# creates mask with 0s wherever there is padding in the input
input_msk = (input_seq != input_pad).unsqueeze(1)

而对于输出序列，除了对padding做处理之外，还要记得屏蔽当前位置之后的信息：

1
2
3
4
5
# create mask as beforetarget_seq = batch.French.transpose(0,1)
target_pad = FR_TEXT.vocab.stoi['<pad>']
target_msk = (target_seq != target_pad).unsqueeze(1)size = target_seq.size(1) # get seq_len for matrixnopeak_mask = np.triu(np.ones(1, size, size),
k=1).astype('uint8')
nopeak_mask = Variable(torch.from_numpy(nopeak_mask) == 0)target_msk = target_msk & nopeak_mask

Multi-Headed Attention

在处理好前面所有的步骤之后，我们可以开始着手搭建网络了，首先开始搭建Multi-Headed Attention部分。

如图所示，在[Self-attention——壹](理解Self-Attention | HelloBear)部分我们详细介绍过了原理，这边直接看代码实现。

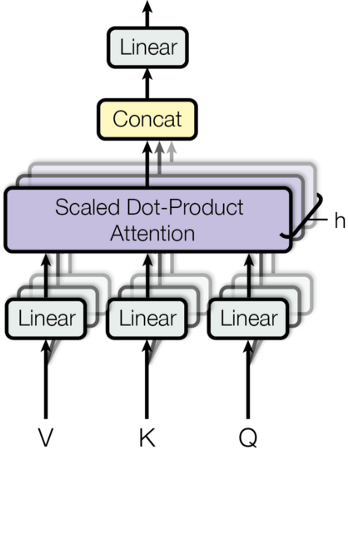
对于$Q,K,V$三个变量，形状都是batch_size * sequence * d_model在多头注意力机制中，我们将变量划分为N-head，得到的向量维数为：batch_size* N * sequence * d_{model/N}，我们将$d_{model}/N$标记为$d_k$，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class MultiHeadAttention(nn.Module):
    def __init__(self, heads, d_model, dropout = 0.1):
        super().__init__()

        self.d_model = d_model
        self.d_k = d_model // heads
        self.h = heads

        self.q_linear = nn.Linear(d_model, d_model)
        self.v_linear = nn.Linear(d_model, d_model)
        self.k_linear = nn.Linear(d_model, d_model)
        self.dropout = nn.Dropout(dropout)
        self.out = nn.Linear(d_model, d_model)

    def forward(self, q, k, v, mask=None):

        bs = q.size(0)

        # perform linear operation and split into h heads

        k = self.k_linear(k).view(bs, -1, self.h, self.d_k)
        q = self.q_linear(q).view(bs, -1, self.h, self.d_k)
        v = self.v_linear(v).view(bs, -1, self.h, self.d_k)

        # transpose to get dimensions bs * h * sl * d_model

        k = k.transpose(1,2)
        q = q.transpose(1,2)
        v = v.transpose(1,2)# calculate attention using function we will define next
        scores = attention(q, k, v, self.d_k, mask, self.dropout)

        # concatenate heads and put through final linear layer
        concat = scores.transpose(1,2).contiguous().view(bs, -1, self.d_model)

        output = self.out(concat)

        return output

Calculating Attention

终于到了计算attention部分了，使用的公式如下：

$$
attention (Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V
$$

示意图如下，首先计算的是Scaled-self-attention，然后再进入Softmax之前，对向量进行一个Mask操作，也就是将padding的部分对于的attention值设置为很小的负数，在decoder中还要屏蔽当前序列之后的值；在softmax之后，如果使用了dropout的话，还要引入dropout。

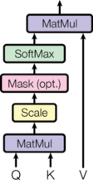
最终的代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def attention(q, k, v, d_k, mask=None, dropout=None):

    scores = torch.matmul(q, k.transpose(-2, -1)) /  math.sqrt(d_k)

    if mask is not None:
        mask = mask.unsqueeze(1)
        scores = scores.masked_fill(mask == 0, -1e9)
        scores = F.softmax(scores, dim=-1)

    if dropout is not None:
        scores = dropout(scores)

    output = torch.matmul(scores, v)
    return output

The Feed-Forward Network

全连接网络很容易，FFN 中的激活函数成为了一个主要的提供非线性变换的单元（另一个来自self-attention中的softmax）。代码：

1
2
3
4
5
6
7
8
9
10
11
class FeedForward(nn.Module):
    def __init__(self, d_model, d_ff=2048, dropout = 0.1):
        super().__init__() 
        # We set d_ff as a default to 2048
        self.linear_1 = nn.Linear(d_model, d_ff)
        self.dropout = nn.Dropout(dropout)
        self.linear_2 = nn.Linear(d_ff, d_model)
    def forward(self, x):
        x = self.dropout(F.relu(self.linear_1(x)))
        x = self.linear_2(x)
        return x

GELU原理？相比ReLU的优点？

  • ReLU会确定性的将输入乘上一个0或者1(当x<0时乘上0，否则乘上1)，

  • Dropout则是随机乘上0，

  • GELU虽然也是将输入乘上0或1，但是输入到底是乘以0还是1，是在取决于输入自身的情况下随机选择的。

什么意思呢？具体来说：

我们将神经元的输入x 乘上一个服从伯努利分布的 m。而该伯努利分布又是依赖于x的：

$$
m \sim Bernoulli(\Phi(x)), where \Phi(x) = P(X \le x)
$$

其中， x服从0为均值，1为方差的高斯分布，那么\Phi就服从标准正态分布的累积分布函数。当x减小时，\Phi的值也会减小，此时x被“丢弃”的可能性更高。所以说这是随机依赖于输入的方式。

现在，给出GELU函数的形式：

$$
GELU(x) = \Phi(x)* I(x) + (1-\Phi(x))*x = x\Phi(x)
$$

因为这个函数没有解析解，所以要用近似函数来表示。图像：

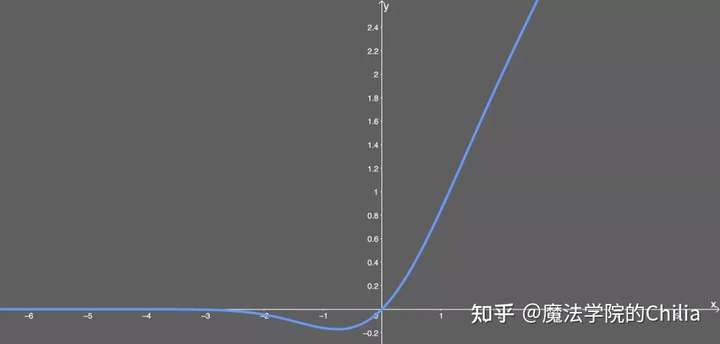
导数形式：

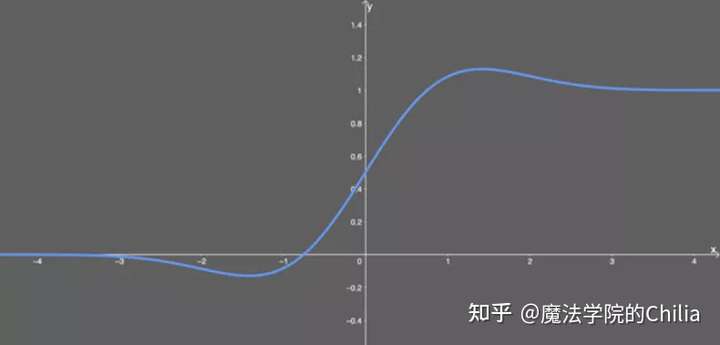
所以，GELU的优点就是在ReLU上增加随机因素，x越小越容易被mask掉

Normalisation

最后，还差一个layer-normalization的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Norm(nn.Module):
    def __init__(self, d_model, eps = 1e-6):
        super().__init__()

        self.size = d_model
        # create two learnable parameters to calibrate normalisation
        self.alpha = nn.Parameter(torch.ones(self.size))
        self.bias = nn.Parameter(torch.zeros(self.size))
        self.eps = eps
    def forward(self, x):
        norm = self.alpha * (x - x.mean(dim=-1, keepdim=True)) \
        / (x.std(dim=-1, keepdim=True) + self.eps) + self.bias
        return norm

以上，就是实现Transformer的全部代码。

为什么要加入残差模块？

  • 动机：因为 transformer 堆叠了 很多层，容易 梯度消失或者梯度爆炸
  • 原因：
    • 数据经过该网络层的作用后，不再是归一化，偏差会越来越大，所以需要将 数据 重新 做归一化处理；
  • 目的：
    • 在数据送入激活函数之前进行normalization（归一化）之前，需要将输入的信息利用 normalization 转化成均值为0方差为1的数据，避免因输入数据落在激活函数的饱和区而出现 梯度消失或者梯度爆炸 问题

参考资料

1 [The Annotated Transformer](The Annotated Transformer)

2 attention-is-all-you-need-pytorch

3 Attention is all your need