HelloBear

Less is More

0%

K-means

Posted on Edited on

K-means是常见的无监督聚类算法，其中k是用户指定的要创建簇的数目。该方法k个随机的质心开始，算法会计算每个点到质心的距离，每个点会被分配到距其最近的簇质心，然后接着基于新分配到的点更新簇质心。

本文介绍该算法的原理以及代码实现。

K-means算法简介

算法原理

对于一组没有标签的数据$x_1$，，，$x_n$，目标是将其划分为K个类别。

每个类别的中心是$\mu_k$，对于每个数据点$x_n$。

引入二值指示变量$r_{nk}=0,1$，其中k的取值为1到n，表示数据点属于K个聚类中的哪一个。

从而如果数据点$x_n$被分配到类别$k$，那么

$$
r_{nk}=1
$$

若$j\ne k$，则

$$
r_{nj}=0
$$

目标函数为失真度量：

$$
J = \sum_{n = 1}^N{\sum_{k = 1}^{K}{r_{nk} |\mathbf{x}_n - \mathbf{\mu}_k |^{2}}}
$$

表示的是每个数据点到与它被分配的向量$\mu_k$之间的距离平方和。为了使得$J$最小化，分两步：

  • E步骤：保持类别中心不变，关于$r_{nk}$最小化目标函数（计算KN次，每次将样本分配给距离最近的中心）

  • M步骤：保持划分结果不变，关于$\mu_{k}$最小化J，即求导数，得到：

    $$
    \mu_{k} = \frac{\sum_{n}{r_{nk}\mathbf{x}_n} }{\sum_n r_nk}
    $$

    即对每个类别内的样本取平均。

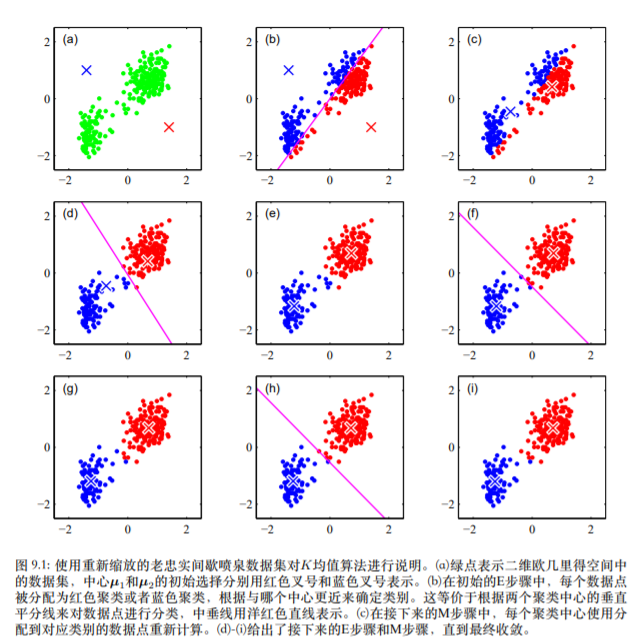
一个二维数据k=2的实际例子如下：

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import random

def distEclud(x1,x2):
    return np.sqrt(np.sum(np.power(x1-x2,2)))

def randCent(dataSet,k):
    n = np.shape(dataSet)[1]
    centroids = np.mat(np.zeros(k,n))
    for j in range(n):
        minJ = min(dataSet[:,j])
        rangeJ = float(max(dataSet[:,j])-minJ)
        centroids[:,j] = minJ + rangeJ * random.rand(k,1)
    return centroids

def kmeans(dataSet,k,distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0]
    clusterAssment = np.mat(zeros((m,2)))
    centroids = createCent(dataSet,k)
    clusterChanged = True
    while clusterChanged: 
        clusterChanged = False
        for i in range(m):
            minDist = inf
            minIndex = -1
            for j in range(k):
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI
                    minIndex = j
            if clusterAssment[i,0] != minIndex:
                clusterChanged = True
            clusterAssment[i,:] = minIndex,minDist**2
        print(centroids)
        for cent in range(k):
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]
            centroids[cent,:] = mean(ptsInClust,axis=0)
    return centroids,clusterAssment

改进K-means

  • 利用后处理来提高聚类性能：用SSE（Sum of Squared Error，误差平方和）来度量聚类的效果，后处理的方法有，将具有最大SSE值的簇划分为两个簇，也可以将两个簇合并为一个簇（合并最近的质心or合并两个使SSE增幅最小的质心）

  • 二分K-means：为了克服K-means算法收敛到局部极小值的问题，有人提出了二分K-means的方法。该算法首先将所有的点作为一个簇，然后将该簇一分为2，之后选择其中的一个簇继续划分。选择待划分的簇的方法有两种，第一是选择那些对其进行划分完可以最大程度减少SSE的簇，第二是选择目前具有最大SSE的簇。

  • 加速K-means：对数据结构的预先计算法使⽤距离的三⾓不等式避免了不必要的距离计算

  • 聚类中心初始化选择：⼀个更好的初始化步骤是将聚类中⼼选择为由K个随机数据点组成的⼦集

  • 在线随机算法：

    $$
    \mu_{k}^新 = \mu_k^旧 + \eta_n(x_n - \mu_k^旧)
    $$

  • K中⼼点算法：

    $$
    \overline{J} = \sum_{n = 1}^N{\sum_{k = 1}^K{r_{nk}\mathcal{V}( x_n,\mathbf{\mu}_k)} }
    $$

    引用新的不相似度度量，E步骤相同，M步骤更复杂

  • 位于两个聚类中⼼的⼤概中间的位置的数据点：使⽤概率的⽅法，我们得到了对数据点聚类的”软”分配

应用

  • 图像分割：不考虑像素的空间上的近似性，下图给出了运⾏K均值算法直⾄收敛的结果。对于任意特定的K值，我们将每个像素的{R,G,B}亮度三元组⽤聚类中心$\mu_{k}$的亮度值替代。

  • 图像压缩：保存每个像素点对应的聚类中心，以及聚类中心即可。

参考资料

1、《模式识别与机器学习》

2、《学习机器实战》学习第10章