对于一个搜索引擎而言，输入一个特定的查询，搜索的结果排名主要取决于两组信息——网页的质量信息（Quality）和相关性信息（Relevance）。

网页质量

PageRank

计算网页质量最为著名的算法是Google的PageRank算法。

互联网上成千上万的网页，这些网页的质量良莠不齐，PageRank就是为了判定这些网页的质量信息的一种方法。该方法的核心思想是如果一个网页被很多其他网页所链接，说明它受到了普遍的承认和信赖，那么他的网页质量就越高。如果把一次超链接座位一次投票，那么某个网页的质量取决于其他网页的投票结果。

对于每个网页而言，除了使用指向自己的链接的数量作为质量分数外，由于指向该网页的不同网页本身的质量也是不一样的，所以最终计算一个网页的得分时，是用所有指向这个网页的其他网页的权重之和。拿投票的例子举例，如果某个网页的质量更可靠，那么它拿到的票数也就多，被它所指向的网页也就意味着质量更可能好了。
下面的图展示了这个意思：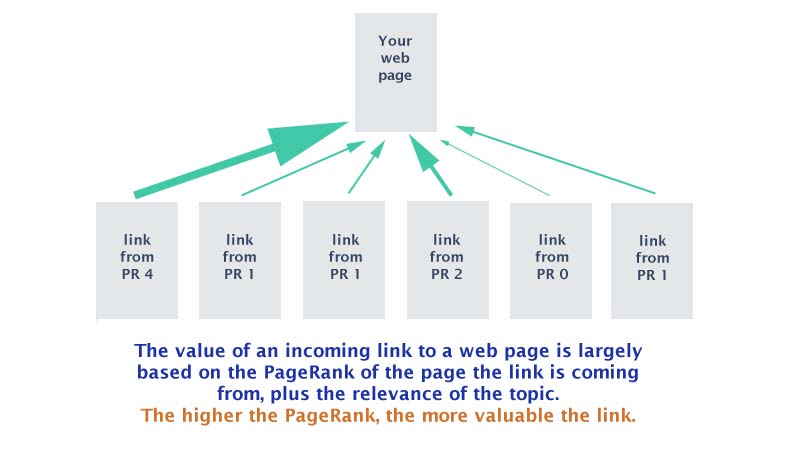

这里如何得到每个网页本身的权重呢？答案是权重就等于网页的质量分数。这就出现了一个问题，该算法本身就是为了计算网页的质量分数，这就造成了死循环。

Google的两位创始人解决这个问题的方法是把这个问题变成二维矩阵相乘的问题，并使用迭代的方法解决。首先假设所有的网页排名是相同的，并根据这个初始值计算出各个网页的的第一次迭代排名，然后根据第一次迭代排名计算第二次的排名，他们从理论上证明了不论初始值如何选择，这种算法都可以保证收敛到真实值。

这种算法的思想来源于将整个互联网作为一个整体看待，使用图论中的节点表征一个网站，网页的链接则代表弧，这样互联网就可以用一个图或者矩阵来表征。

计算方法

下面具体介绍一下PageRank算法的计算方式。

假定向量：
$$
B = (b_1, b2, …, b_N) ^t
$$
为第一、第二直到第N个网页的排名。矩阵
$$
A =
\begin{gathered}

\begin{bmatrix} a_{11} & … & a_{1n} & … & a_{1M} \
… & & & & … \
a_{m1} & … & a_{mn} & … & a_{mM} \
… & & & & … \
a_{M1} & … & a_{Mn} & … & a_{MM} \
\end{bmatrix}

\end{gathered}
$$
是网页之间的链接数目，其中 $a_{mn}$ 代表第m个网页指向第n个网页的链接数。A是已知的，B是未知的，即需要计算的结果。

假定$B_i$是第i次迭代的结果，那么：
$$
B_i = A * B_{i-1}
$$
开始假定所有的网页排名都是一样的，即：
$$
B_0 = (\frac{1}{N}, \frac{1}{N}, … , \frac{1}{N})
$$
通过反复的迭代，可以证明$B_i$最终会收敛，即满足：
$$
B = B * A
$$
实际计算的时候，只需要判断几次迭代之间的差异值非常小的时候就可以停止了，一般10次左右即可停止。

由于网页之间链接的数量比互联网的规模而言非常的少，也就导致矩阵非常的稀疏。所以此时加入了一个很小的平滑因子$\alpha$，用于对零概率或者小概率事件进行平滑处理，此时迭代公式变为：
$$
B_i = [\frac{\alpha}{N}* I + (1-\alpha) * A] * B_{i-1}
$$
其中N是互联网网页的数量，$\alpha$ 取值一般是0.15，$ I $是单位矩阵。

矩阵的乘法通过分块矩阵的计算方式，使用MapReduce计算工具可以加速计算。

代码实现

参考自wikipedia：

"""PageRank algorithm with explicit number of iterations.

Returns
-------
ranking of nodes (pages) in the adjacency matrix

"""

import numpy as np

def pagerank(M, num_iterations: int = 100, d: float = 0.85):
    """PageRank: The trillion dollar algorithm.

    Parameters
    ----------
    M : numpy array
        adjacency matrix where M_i,j represents the link from 'j' to 'i', such that for all 'j'
        sum(i, M_i,j) = 1
    num_iterations : int, optional
        number of iterations, by default 100
    d : float, optional
        damping factor, by default 0.85

    Returns
    -------
    numpy array
        a vector of ranks such that v_i is the i-th rank from [0, 1],
        v sums to 1

    """
    N = M.shape[1]
    v = np.ones(N) / N
    M_hat = (d * M + (1 - d) / N)
    for i in range(num_iterations):
        v = M_hat @ v
    return v

M = np.array([[0, 0, 0, 0, 1],
              [0.5, 0, 0, 0, 0],
              [0.5, 0, 0, 0, 0],
              [0, 1, 0.5, 0, 0],
              [0, 0, 0.5, 1, 0]])
v = pagerank(M, 100, 0.85)

HelloBear

经典搜索方法

网页质量

PageRank

计算方法

代码实现

相关性

TF-IDF